How to Solve Gamma Function
I. Theoretical Analysis
Gamma Function is defined in the following,
\[\Gamma(n) = \int_{0}^{\infty} \mathrm{e}^{-x}x^{n-1}\mathrm{d}x.\]Using integration by parts, one sees that:
\[\Gamma(n) = -[\mathrm{e}^{-x}x^{n-1}]_0^{\infty} + (n-1)\int_{0}^{\infty} \mathrm{e}^{-x}x^{n-2}\mathrm{d}x = (n-1)\Gamma(n-1).\]From the above calculation,and note that
\[\Gamma(1) = \int_{0}^{\infty} \mathrm{e}^{-x}\mathrm{d}x = 1\\ \Gamma(1/2) = \int_{0}^{\infty} \mathrm{e}^{-x}x^{-1/2}\mathrm{d}x = 2\int_{0}^{\infty} \mathrm{e}^{-y^2}\mathrm{d}y = \sqrt{\pi},\]where \(y^2 = x\).
If \(n\) is a positive integer, one can obtain:
\[\Gamma(n) = (n-1)(n-2)\cdots 1 \cdot \Gamma(1) = (n-1)!,\] \[\Gamma(n+\frac{1}{2}) = (n-\frac{1}{2})(n-\frac{3}{2})\cdots\frac{1}{2}\Gamma(\frac{1}{2})= (n-\frac{1}{2})(n-\frac{3}{2})\cdots\frac{1}{2}\sqrt{\pi}.\]Appendix:
Integral calculus(\(y\equiv \sqrt{a}[x+(b/2a)]\))
\[\int_{-\infty}^{+\infty}\mathrm{e}^{-(ax^2+bx)}\mathrm{d}x = \int_{-\infty}^{+\infty}\mathrm{e}^{-y^2 + (b^2/4a)}\frac{1}{\sqrt{a}}\mathrm{d}y = \frac{1}{\sqrt{a}}\mathrm{e}^{b^2/4a}\int_{-\infty}^{+\infty}\mathrm{e}^{-y^2}\mathrm{d}y = \boxed{\sqrt{\frac{\pi}{a}}\mathrm{e}^{b^2/4a}}.\]If it meets a condition \(e^{-x^2} > 0\), obviously given that,
\[I = \int_{-\infty}^{\infty} e^{-x^2} \mathrm{d}x > 0,\]Calculate quadratic \(I^2\),
\[I^2 = \int_{-\infty}^{\infty} e^{-x^2} \mathrm{d}x \int_{-\infty}^{\infty} e^{-y^2} \mathrm{d}y = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{\left(-x^2 - y^2 \right)} \mathrm{d}x\mathrm{d}y,\]Using integration by polar coordinates, \(x = r \cos {\theta}, y = r \sin {\theta}\), and,
\[dxdy = \frac{D\left({x,y}\right)}{D\left( {r,\theta} \right)} \mathrm{d}r\mathrm{d}\theta = \left| { \begin{array}{*{20}{cc}} {\frac{\partial x}{\partial r}}&{\frac{\partial x}{\partial \theta }}\\ {\frac{\partial y}{\partial r}}&{\frac{\partial y}{\partial \theta }} \end{array}} \right|\mathrm{d}r\mathrm{d}\theta = \left| {\begin{array}{*{20}{cr}} {\cos \theta }&{ - r\sin \theta }\\ {\sin \theta }&{r\cos \theta } \end{array}} \right|drd\theta = r\mathrm{d}r\mathrm{d}\theta,\]then, one sees that
\[I^2 = \int_{0}^{\infty}\int_{0}^{2\pi}e^{-{r^2}}r\mathrm{d}r\mathrm{d}{\theta} = \int_{0}^{\infty}e^{-{r^2}}r\mathrm{d}r\int_{0}^{2\pi}\mathrm{d}{\theta} = \frac{1}{2} \times 2\pi = \pi,\]Therefore,
\[I = \int_{-\infty}^{\infty} e^{-x^2} \mathrm{d}x = \boxed{\sqrt{\pi}}.\]II. Numerical analysis
Evaluate Gamma function in matlab.
1.Evaluate the gamma function with a scalar and a vector.
>> y = gamma(0.5)
y =
1.7725
>> y = gamma(-pi:pi)
y =
1.0157 -3.1909 6.8336 -7.8012 1.1046 0.9482 1.7621
2.Plot the gamma function and its inverse.
% PlotGammaFunctionExample.m
fplot(@gamma)
hold on
fplot(@(x) 1./gamma(x))
legend('\Gamma(x)','1/\Gamma(x)')
hold off
grid on
Figure.
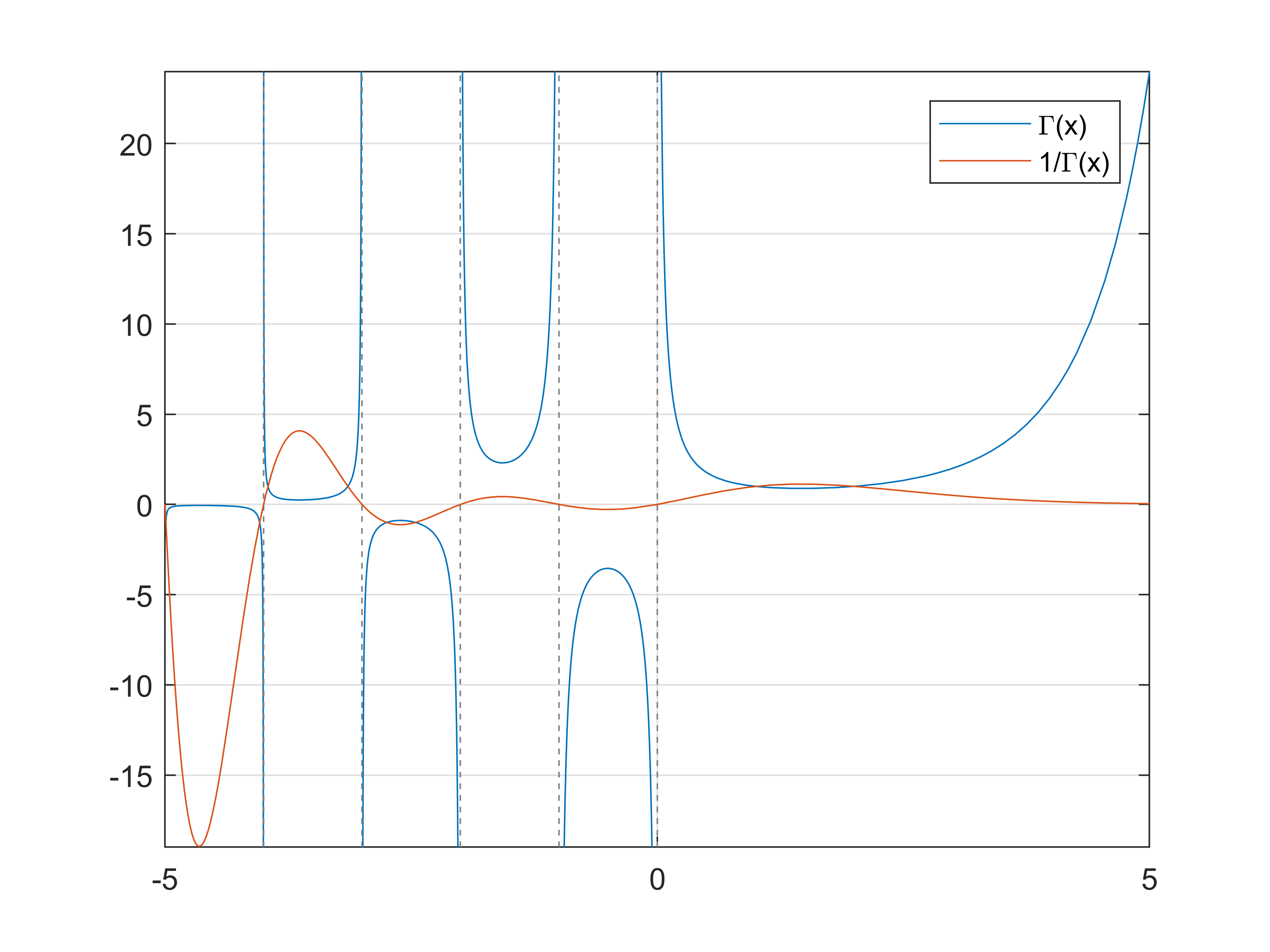
In addition, the domain of the gamma function extends to negative real numbers by analytic continuation, with simple poles at the negative integers. This extension arises from repeated application of the recursion relation
\[\Gamma(n-1) = \frac{\Gamma(n)}{n-1}.\]More information see here.
Related article maybe useful to you: